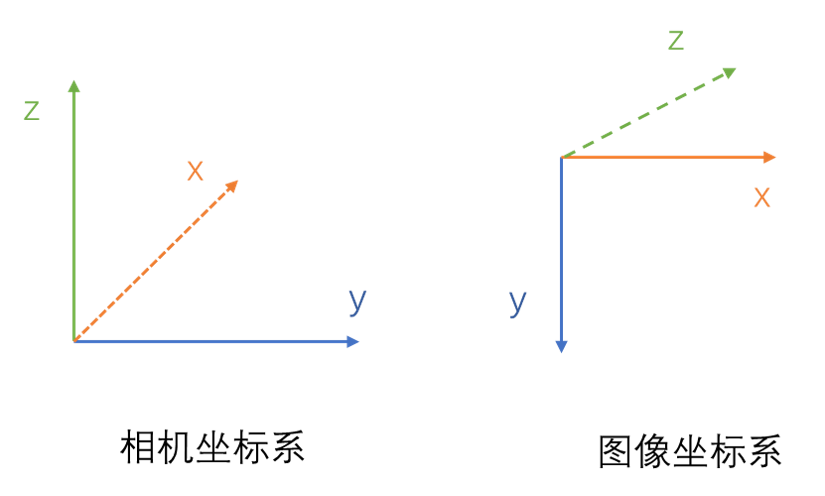Carla的坐标变换
carla仿真器是基于unreal引擎的,因此底层的世界坐标也是unreal的世界坐标系。
为了完成毕设任务,需要去了解carla每个actor之间的坐标变换。如每个相机间的相对位置,车辆与相机的相对位置。
总体上carla的坐标系方向为:x->forward, y->right, z->height
系统的原点即为location:(0,0,0),Orientation:(0,0,0)
那么每一个transform即为相对世界原点的坐标变换,同时也就是世界坐标
理解了上一句话对于整体的理解就很重要了(我是最后才明白了这个,一下子就豁然开朗了)
相对坐标变换
直接上官方的样例代码。
1
2
3
4
5
6
7
8
9
10
11
12
| @staticmethod
def get_bounding_box(vehicle, camera):
"""
Returns 3D bounding box for a vehicle based on camera view.
"""
bb_cords = ClientSideBoundingBoxes._create_bb_points(vehicle)
cords_x_y_z = ClientSideBoundingBoxes._vehicle_to_sensor(bb_cords, vehicle, camera)[:3, :]
cords_y_minus_z_x = np.concatenate([cords_x_y_z[1, :], -cords_x_y_z[2, :], cords_x_y_z[0, :]])
bbox = np.transpose(np.dot(camera_coordinate(camera), cords_y_minus_z_x))
camera_bbox = np.concatenate([bbox[:, 0] / bbox[:, 2], bbox[:, 1] / bbox[:, 2], bbox[:, 2]], axis=1)
return camera_bbox
|
分别介绍每一句意义
1
| _create_bb_points(vehicle) #获取了车辆的局部坐标系下的三维框的每一个顶点,局部坐标系原点就是3D框的几何中心
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| @staticmethod
def _create_bb_points(vehicle):
"""
Returns 3D bounding box for a vehicle.
"""
cords = np.zeros((8, 4))
extent = vehicle.bounding_box.extent
cords[0, :] = np.array([extent.x, extent.y, -extent.z, 1])
cords[1, :] = np.array([-extent.x, extent.y, -extent.z, 1])
cords[2, :] = np.array([-extent.x, -extent.y, -extent.z, 1])
cords[3, :] = np.array([extent.x, -extent.y, -extent.z, 1])
cords[4, :] = np.array([extent.x, extent.y, extent.z, 1])
cords[5, :] = np.array([-extent.x, extent.y, extent.z, 1])
cords[6, :] = np.array([-extent.x, -extent.y, extent.z, 1])
cords[7, :] = np.array([extent.x, -extent.y, extent.z, 1])
return cords
|
下一句:
1
| ClientSideBoundingBoxes._vehicle_to_sensor(bb_cords, vehicle, camera)[:3, :]
|
将车辆的bbox坐标转换到了相机
1
2
3
4
5
6
7
8
9
| @staticmethod
def _vehicle_to_sensor(cords, vehicle, sensor):
"""
Transforms coordinates of a vehicle bounding box to sensor.
"""
world_cord = ClientSideBoundingBoxes._vehicle_to_world(cords, vehicle)
sensor_cord = ClientSideBoundingBoxes._world_to_sensor(world_cord, sensor)
return sensor_cord
|
分别是车辆到世界,世界再到相机,思路很清晰,先看第一个。
1
2
3
4
5
6
7
8
9
10
11
| @staticmethod
def _vehicle_to_world(cords, vehicle):
"""
Transforms coordinates of a vehicle bounding box to world.
"""
bb_transform = carla.Transform(vehicle.bounding_box.location)
bb_vehicle_matrix = ClientSideBoundingBoxes.get_matrix(bb_transform)
vehicle_world_matrix = ClientSideBoundingBoxes.get_matrix(vehicle.get_transform())
bb_world_matrix = np.dot(vehicle_world_matrix, bb_vehicle_matrix)
world_cords = np.dot(bb_world_matrix, np.transpose(cords))
return world_cords
|
获取了车辆boundingbox的一个局部转换(boundingbox是相对车辆坐标系的,重复强调)
get_matrix将这个转换变换为了变换矩阵形式(平移旋转4×4的矩阵)
之后再获得车辆世界坐标系下的变换矩阵,点乘车辆世界变换矩阵和局部的boungdingbox的变换矩阵,获得了boundingbox到世界的变换矩阵。
1
2
3
4
5
6
7
8
9
10
| @staticmethod
def _world_to_sensor(cords, sensor):
"""
Transforms world coordinates to sensor.
"""
sensor_world_matrix = ClientSideBoundingBoxes.get_matrix(sensor.get_transform())
world_sensor_matrix = np.linalg.inv(sensor_world_matrix)
sensor_cords = np.dot(world_sensor_matrix, cords)
return sensor_cords
|
之后将世界转换到相机坐标系下,同样的思路,获得世界坐标系下相机的世界矩阵(重复强调,就是相对于世界原点的变换矩阵)
将这个世界(变换)矩阵求逆,就得到了将世界到相机坐标系下的变换矩阵,通过左乘世界坐标系下的世界坐标,将这个世界坐标转换到了相机坐标系下。从变量名看,sensor_world为相机到世界,逆就是world_sensor了嘛。
注意输入的cord是一个8×4的局部坐标矩阵(第四维为补的1),输出为4×8(转置 了),主函数中取[:3,:]即获取了xyz的世界坐标。
carla定义的Transform就是一个变换,输出我设置的一个相机的世界Transform
1
| Transform(Location(x=-67,y=-126.5,z=5.0),Rotation(pitch=-14.999996,yaw=155.000031,roll=0.00000))
|
使用get_matrix将这个变换转换成了三维世界下的变换矩阵(4×4)。
相机坐标转图像坐标
1
| cords_y_minus_z_x = np.concatenate([cords_x_y_z[1, :], -cords_x_y_z[2, :], cords_x_y_z[0, :]])
|
这一句将相机坐标系下的坐标进行图像坐标轴的变换。
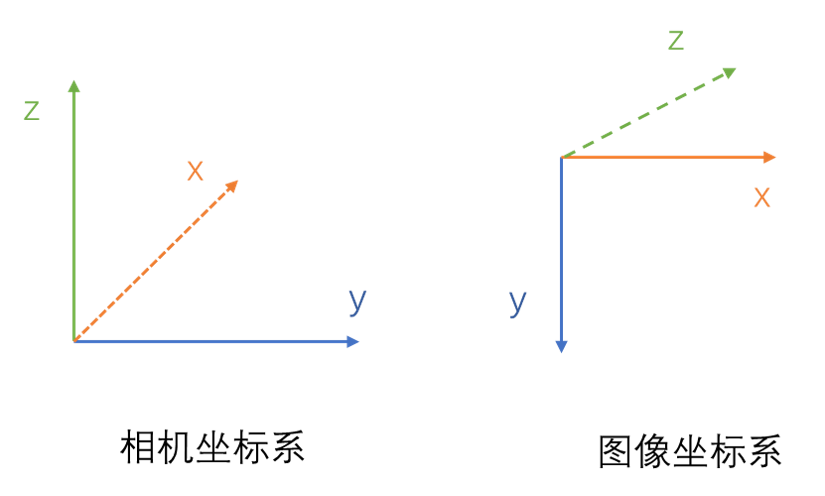
y变x,-z变y,x变z
1
| bbox = np.transpose(np.dot(camera_coordinate(camera), cords_y_minus_z_x))
|
使用相机内参矩阵将相机坐标系下的坐标变换为图像坐标系下的坐标。
主函数最后返回8×3的图像坐标,第三维为1,前两维分别是图像(x,y)
结束啦!
3月23晚21点更新
突然发现事情没有这么简单。
生成数据集时已经对坐标系进行了变换,即按照上图所示使用的是图像坐标系下的三维坐标。
因此在读取数据后,需要进行坐标变换,将KITTI格式的GT从图像坐标系变换到相机坐标系下
做法就是:
x = location[‘z’]
y = location[‘x’]
z = -location[‘y’]
若没有进行坐标变换则进行坐标系矩阵乘法后结果直接没用(必然的)
这个变换后[x,y,z,1]就是相机source坐标系下的点,需要得到target坐标系下的坐标[x’,y’,z’,1]
有了前面的总结,可以容易的知道:
[x’,y’,z’,1] = inv(target_matrix) · source_matrix · transpose([x,y,z,1])
最后这么算结果正确。
变换完的坐标系仍然是相机坐标系,还需要转换为图像坐标系与KITTI数据保持一致。
值得注意的是,实验中保留了GT的小数点后四位,转换后坐标存在0.1m的误差,如果要转换精度高在制作数据集时保留更多的位数。